篇首语:本文由编程笔记#小编为大家整理,主要介绍了数据结构C语言 《四》二叉树,堆的基本概念以及堆的相关操作实现(上)相关的知识,希望对你有一定的参考价值。

树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
树也可以这样定义:树是由根节点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的节点,所定义的关系称为父子关系。父子关系在树的节点之间建立了一个层次结构。在这种层次结构中有一个节点具有特殊的地位,这个节点称为该树的根节点,或称为树根。
空集合也是树,称为空树。空树中没有节点;
孩子节点或子节点:一个节点含有的子树的根节点
节点的度:一个节点含有的子节点的个数
叶节点或终端节点:度为0的节点
非终端节点或分支节点:度不为0的节点;
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
兄弟节点:具有相同父节点的节点互称为兄弟节点;
树的度:最大的节点的度
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次;
堂兄弟节点:双亲在同一层的节点互为堂兄弟;
节点的祖先:从根到该节点所经分支上的所有节点;
子孙:以某节点为根的子树中任一节点都称为该节点的子孙;
森林:由m(m>0)棵互不相交的树的集合称为森林;
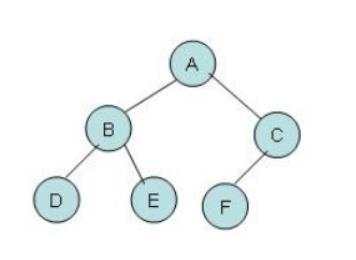
二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个结点。
二叉树的特点:
特殊的二叉树:
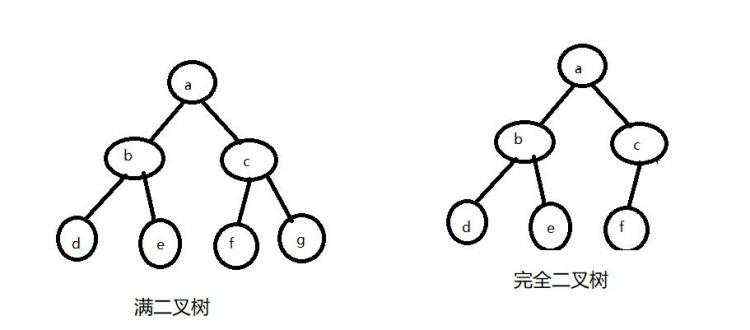
当i=1时,该节点为根,它无双亲节点 。
当i>1时,该节点的双亲节点的编号为i/2 。
若2i≤n,则有编号为2i的左节点,否则没有左节点 。
若2i+1≤n,则有编号为2i+1的右节点,否则没有右节点
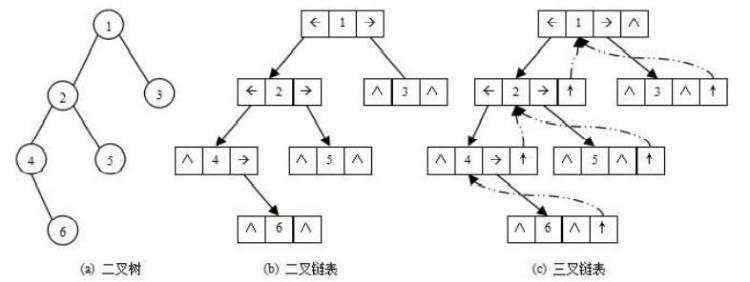
前序/中序/后序的递归结构遍历:是根据访问结点操作发生位置命名
简而言之
| 方式 | 顺序 |
|---|---|
| 前序遍历 | 根、左、右 |
| 中序遍历 | 左、根、右 |
| 后序遍历 | 左、右、根 |
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
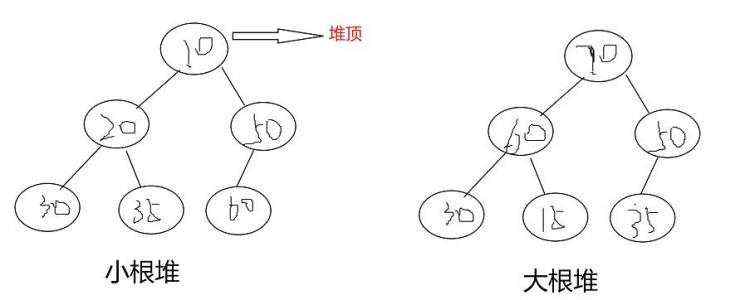
如果有一个关键码的集合K &#61; k0&#xff0c;k1&#xff0c; k2&#xff0c;…&#xff0c;kn-1&#xff0c;把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中&#xff0c;并满足&#xff1a;Ki <&#61; K2i&#43;1 且 Ki<&#61; K2i&#43;2 (Ki >&#61; K2i&#43;1 且 Ki >&#61; K2i&#43;2) i &#61; 0&#xff0c;1&#xff0c;2…&#xff0c;则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆&#xff0c;根节点最小的堆叫做最小堆或小根堆。
堆的性质&#xff1a;
1.堆中某个节点的值总是不大于或不小于其父节点的值&#xff1b;
2.堆总是一棵完全二叉树。
Heap.h
#pragma once
typedef int DataType;
//定义一个函数指针类型&#xff0c;用来选择大小堆实现方式
typedef int(*PCompare)(DataType left, DataType right);
typedef struct Heap
DataType *arr;
int capacity;
int size;
PCompare PCOM; //函数指针变量&#xff0c;来指向所有比较函数
Heap;
//小堆方式
int Less(DataType child, DataType parent);
//大堆方式
int Greater(DataType child, DataType parent);
//堆的初始化
void HeapInit(Heap *hp, DataType *arr, int size,PCompare PCOM);
//堆的插入
void HeapInsert(Heap *hp, DataType x);
//堆的删除
void HeapDelete(Heap *hp);
//获取堆顶元素
DataType HeapTop(Heap *hp);
//获取堆中有效元素个数
int HeapSize(Heap *hp);
//判空
int HeapEmpty(Heap *hp);
//堆的销毁
void HeapDestroy(Heap * hp);
//堆排序
void HeapSort(int arr[],int size);
//TOP-K问题
void PrintTopK(int* a, int n, int k);
void TestTopk();
void TestHeap();
Heap.c
#include"Heap.h"
#include
#include
#include
//小堆方式
int Less(DataType child, DataType parent)
return child < parent;
//大堆方式
int Greater(DataType child, DataType parent)
return child > parent;
//交换
void Swap(DataType *left, DataType *right)
DataType tmp &#61; *left;
*left &#61; *right;
*right &#61; tmp;
//向下调整&#xff08;大堆&#xff09;
void AdjustDown(Heap *hp, int parent)
DataType *arr &#61; hp->arr;
int size &#61; hp->size;
// 默认child标记左孩子&#xff0c;parent的右孩子可能不存在
int child &#61; parent * 2 &#43; 1;
while (child<size)
//在右孩子存在的情况下&#xff0c;找到左右孩子中最小的
if (child &#43; 1 < size && hp->PCOM(arr[child &#43; 1] , arr[child]))
child &#43;&#61; 1;
//检测双亲此时是否满足堆的特性
if (hp->PCOM(arr[child] , arr[parent]))
Swap(&arr[child], &arr[parent]);
//较大的双亲向下移动&#xff0c;可能会导致其子树不满足堆的特性&#xff0c;则还需要继续向下调整
parent &#61; child;
child &#61; parent * 2 &#43; 1;
else
return;
//向上调整&#xff08;小堆&#xff09;
void AdjustUp(Heap *hp)
DataType *arr &#61; hp->arr;
int child &#61; hp->size - 1;
int parent &#61; (child - 1) / 2;
while (child)
if (hp->PCOM(arr[child] , arr[parent]))
Swap(&arr[child], &arr[parent]);
child &#61; parent;
parent &#61; (child - 1) / 2;
else
return;
//堆的初始化
void HeapInit(Heap *hp, DataType *arr, int size, PCompare PCOM)
assert(hp);
hp->arr &#61; (DataType *)malloc(sizeof(DataType)*size);
if (hp->arr &#61;&#61; NULL)
assert(0);
return;
hp->capacity &#61; size;
//将元素逐个拷进来
for (int i &#61; 0; i < size; i&#43;&#43;)
hp->arr[i] &#61; arr[i];
hp->size &#61; size;
hp->PCOM &#61; PCOM;
//1.找倒数第一个非叶子结点
int LastNotLeafNode &#61; ((size - 1) - 1) / 2;
//2.从该节点开始一直到根结点&#xff0c;逐个往前对每个节点进行向下调整
for (int root &#61; LastNotLeafNode; root >&#61; 0; root--)
AdjustDown(hp,root);
//扩容
void CheckCapacity(Heap *hp)
if (hp->size &#61;&#61; hp->capacity)
hp->arr &#61; (DataType *)realloc(hp->arr, sizeof(DataType)*hp->size * 2);
if (hp->arr &#61;&#61; NULL)
assert(0);
return ;
hp->capacity *&#61; 2;
//堆的插入
void HeapInsert(Heap *hp, DataType x)
CheckCapacity(hp);
//1.将元素先插入有效元素之后
hp->arr[hp->size&#43;&#43;] &#61; x;
//2.新元素插入后可能会破坏堆的特性&#xff0c;则还需要对堆进行调整
AdjustUp(hp);
//堆的删除
void HeapDelete(Heap *hp)
if(HeapEmpty(hp))
return;
//将堆顶元素与堆中最后一个元素交换
Swap(&hp->arr[0], &hp->arr[hp->size - 1]);
//将堆中有效元素个数减一
hp->size -&#61; 1;
//将堆顶元素向下调整
AdjustDown(hp, 0);
//获取堆顶元素
DataType HeapTop(Heap *hp)
assert(!HeapEmpty(hp));
return hp->arr[0];
//获取堆中有效元素个数
int HeapSize(Heap *hp)
assert(hp);
return hp->size;
//判空
int HeapEmpty(Heap *hp)
assert(hp);
return hp->size &#61;&#61; 0;
//堆的销毁
void HeapDestroy(Heap * hp)
assert(hp);
if (hp->arr)
free(hp->arr);
hp->arr &#61; NULL;
hp->capacity &#61; 0;
hp->size &#61; 0;
//堆排序的向下调整
void HeapAdjust(int arr[], int size, int parent)
int child &#61; parent * 2 &#43; 1;
while (child < size)
if (child &#43; 1 < size &&arr[child &#43; 1] > arr[child])
child &#43;&#61; 1;
if (arr[child]>arr[parent])
int tmp &#61; arr[child];
arr[child] &#61; arr[parent];
arr[parent] &#61; tmp;
parent &#61; child;
child &#61; 2 * parent &#43; 1;
else
return;
//堆排序
void HeapSort(int arr[],int size)
//1.建堆 大堆升序&#xff0c;小堆降序
int end &#61; size - 1;
for (int root &#61; (size-2) / 2; root >&#61; 0; root--)
HeapAdjust(arr, size, root);
//2.利用堆删除的思想进行排序
while (end>0)
Swap(&arr[end], &arr[0]);
HeapAdjust(arr, end, 0);
end--;
//TOP-K问题&#xff0c;利用堆来处理&#xff0c;时间复杂度O&#xff08;N&#xff09;
//找最大的元素就建小堆&#xff0c;使用前k个元素来建堆&#xff0c;剩下N-k个元素依次与堆顶元素比较
//如果该元素比堆顶元素大&#xff0c;则用该元素替换掉堆顶元素
//1.找最大的K个元素&#xff0c;同理也可以找最小的k个元素&#xff0c;这里就不一一演示了
void PrintTopK(int* a, int n, int k)
Heap hp;
HeapInit(&hp, a, k,Less);
for (int i &#61; k; i < n; i&#43;&#43;)
//每次和堆顶元素比较&#xff0c;大于堆顶元素&#xff0c;则删除堆顶元素&#xff0c;插入新的元素
if (a[i]>HeapTop(&hp))
HeapDelete(&hp);
HeapInsert(&hp, a[i]);
for (int i &#61; 0; i < k; i&#43;&#43;)
printf("%d ", HeapTop(&hp));
HeapDelete(&hp);
printf("\\n");
HeapDestroy(&hp);
void TestHeap()
int arr[] &#61; 5, 6, 2, 4, 1, 7, 3, 9, 8 ;
Heap hp;
HeapInit(&hp, arr, sizeof(arr) / sizeof(arr[0]),Greater);
printf("top&#61; %d\\n",HeapTop(&hp));
printf("size&#61; %d\\n", HeapSize(&hp));
HeapInsert(&hp, 10);
printf("top&#61; %d\\n", HeapTop(&hp));
printf("size&#61; %d\\n", HeapSize(&hp));
HeapDelete(&hp);
printf("top&#61; %d\\n", HeapTop(&hp));
printf("size&#61; %d\\n", HeapSize(&hp));
HeapDestroy(&hp);
#include"Heap.h"
int main()
//TestHeap();
//int arr1[] &#61; 5, 6, 2, 4, 1, 7, 3, 9, 8 ;
//HeapSort(arr1,sizeof(arr1)/sizeof(arr1[0]));
TestTopk();
return 0;
TOP-k问题&#xff0c;自主实现

void SwapTopk(int *left, int *right)
int tmp &#61; *left;
*left &#61; *right;
*right &#61; tmp;
//向下调整
void TOPk(int arr[], int size,int parent)
int child &#61; parent * 2 &#43; 1;
while (child < size)
if (child &#43; 1 < size &&arr[child &#43; 1] < arr[child])
child &#43;&#61; 1;
if (arr[child]<arr[parent])
SwapTopk(&arr[child], &arr[parent]);
parent &#61; child;
child &#61; 2 * parent &#43; 1;
else
return;
void PrintTopK(int* a, int n, int k)
TOPk(a, k,0);
for (int i &#61; k; i < n; i&#43;&#43;)
if (a[i] > a[0])
SwapTopk(&a[i], &a[0]);
TOPk(a, k,0);
for (int i &#61; 0; i < k; i&#43;&#43;)
for (int j &#61; 0; j < k-i; j&#43;&#43;)
if (a[j]

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有